Stellar parallax:
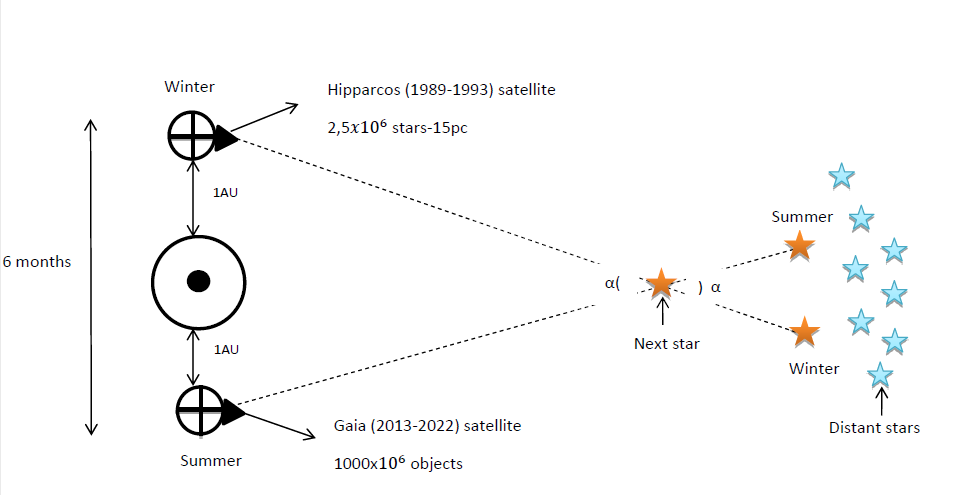
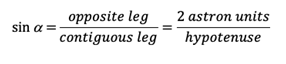
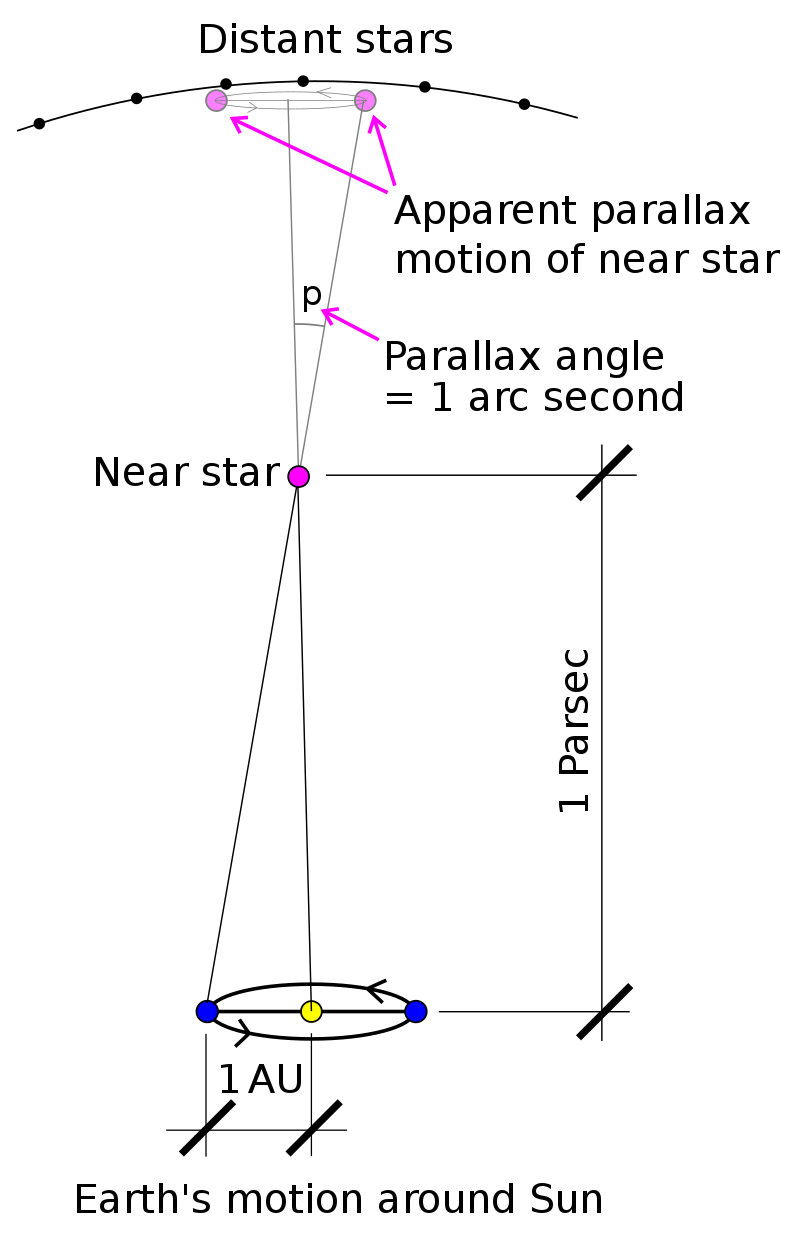
The most accurate method of measuring the distance to stars is called stellar parallax, and it is nothing more than a very accurate trigonometric result. If we stop in a place on our planet and look at the planets for example, and at the same time another person in a distant place does the same, we will see that there seems to be a small lag in the position of the planet with respect to the background stars . But to measure the distances to the stars we have to consider that the Earth revolves around the sun, and this movement should cause the closest stars to move with respect to the farthest ones. So, if we can measure the angle of motion of the nearby star with two measurements 6 months apart, and knowing the distance to the Sun, we can, by simple trigonometry, measure the distance to that star.
This method works only for very short distances because it is not easy to calculate very small angles.
Henrietta Leavitt (1912) realized that stars 10,000 times brighter than the sun existed because they were seen in the Magellanic galaxies. The stars were variable and were called Cepheids because they were discovered in the constellation Cepheus.
Some of the nearby stars, if you look at a difference of months (winter-summer (6 months)) you can see that they have been able to move a little. Their distance has changed.
When powerful telescopes appeared, to discover more about the stars, what they did was look at the stars separately in time (more or less long periods) and took photos to compare them.
Absolute magnitude: internal energy of nuclear fusion of the star shines.
Apparent magnitude: it is the brilliance that we can see from the earth.
To find out which stars are the brightest, what you have to do is put all the stars at the same distance (32 light years) in order to see which star shines brightest and which star shines less.
The brighter the star, the smaller the magnitude number (more negative numbers). The less bright the star, the greater the magnitude number (more positive numbers).
Between two stars apparently of the same luminosity looking from the earth, the one that changes more (the one that moves more) needs more energy to shine because it is further away, and therefore, the magnitude is greater (more negative numbers).
Parallax method:
Throughout the year the position of a star S is noted in relation to other stars in its apparent neighborhood:
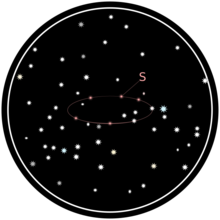
Stars that did not seem to move in relation to each other are used as reference points to determine the path of S.
The observed path is an ellipse: the projection of Earth’s orbit around the Sun through S onto the distant background of non-moving stars. The farther S is removed from Earth’s orbital axis, the greater the eccentricity of the path of S. The center of the ellipse corresponds to the point where S would be seen from the Sun:
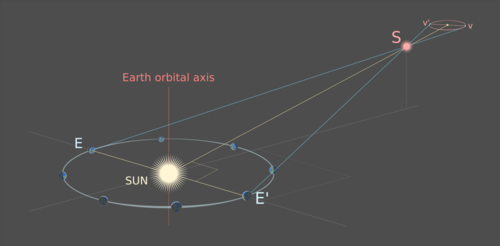
The plane of Earth’s orbit is at an angle to a line from the Sun through S. The vertices v and v' of the elliptical projection of the path of S are projections of positions of Earth E and E’ such that a line E-E’ intersects the line Sun-S at a right angle; the triangle created by points E, E’ and S is an isosceles triangle with the line Sun-S as its symmetry axis.
Any stars that did not move between observations are, for the purpose of the accuracy of the measurement, infinitely far away. This means that the distance of the movement of the Earth compared to the distance to these infinitely far away stars is, within the accuracy of the measurement, 0. Thus a line of sight from Earth's first position E to vertex v will be essentially the same as a line of sight from the Earth's second position E' to the same vertex v, and will therefore run parallel to it - impossible to depict convincingly in an image of limited size:
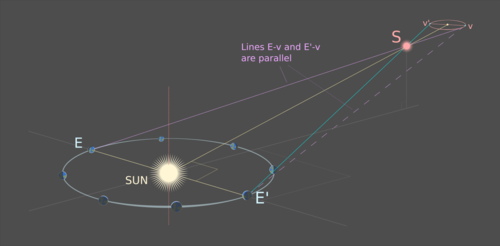
.png)
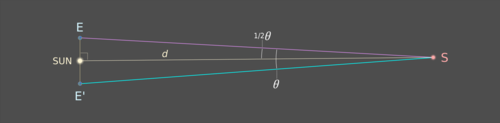
The distance d from the Sun to S now follows from simple trigonometry:
tan(½θ) = E-Sun / d,
so that d = E-Sun / tan(½θ), where E-Sun is 1 AU.
The more distant an object is, the smaller its parallax.
Stellar parallax measures are given in the tiny units of arcseconds, or even in thousandths of arcseconds (milliarcseconds). The distance unit parsec is defined as the length of the leg of a right triangle adjacent to the angle of one arcsecond at one vertex, where the other leg is 1 AU long. Because stellar parallaxes and distances all involve such skinny right triangles, a convenient trigonometric approximation can be used to convert parallaxes (in arcseconds) to distance (in parsecs). The approximate distance is simply the reciprocal of the parallax: For example, Proxima Centauri (the nearest star to Earth other than the Sun), whose parallax is 0.7685, is 1 / 0.7685 parsecs = 1.301 parsecs (4.24 ly) distant.